|
Note: As before, don't take this diagram too literally! It is a composite of several diagrams from different sources, nearly all of which give slightly different boundaries between the different named sorts of radiation. You also mustn't think that this is what the spectrum would actually look like if you were to observe it. The problem lies in the way the scales are drawn. Neither the wavelength nor the frequency scales are simple linear scales - the gap between 102 and 104 is not the same as between 10-2 and 10-4, for example (although they are dawn as the same in the diagram). Work it out! One gap is the difference between 100 and 10,000 (in other words 9,900); the other works out at only 0.0099! That means that in some parts, the spectrum should really be very stretched out, and in others very, very compressed. And because the wavelength and frequency scales are heading in opposite directions, the stretching or compression would be totally different depending on whether you were plotting the spectrum against wavelength or frequency.
Does any of this matter for chemistry purposes? No! Think of the last diagram just as a visual way of placing the various types of radiation relative to each other - it is not a picture of what the spectrum actually looks like.
A DOUBLE BEAM UV-VISIBLE ABSORPTION SPECTROMETER This page describes a double beam UV-visible absorption spectrometer in enough detail to meet the requirements of UK-based chemistry courses for 16 - 18 year olds.
The overall design What you are trying to do
If you pass white light through a coloured substance, some of the light gets absorbed. A solution containing hydrated copper(II) ions, for example, looks pale blue because the solution absorbs light from the red end of the spectrum. The remaining wavelengths in the light combine in the eye and brain to give the appearance of cyan (pale blue).
Some colourless substances also absorb light - but in the ultra-violet region. Since we can't see UV light, we don't notice this absorption.
Different substances absorb different wavelengths of light, and this can be used to help to identify the substance - the presence of particular metal ions, for example, or of particular functional groups in organic compounds.
The amount of absorption is also dependent on the concentration of the substance if it is in solution. Measurement of the amount of absorption can be used to find concentrations of very dilute solutions.
An absorption spectrometer measures the way that the light absorbed by a compound varies across the UV and visible spectrum.
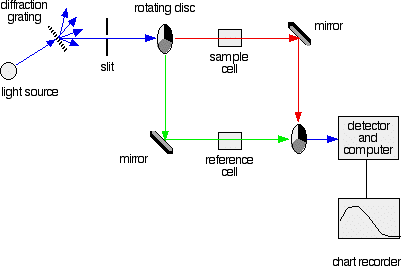
A simple double beam spectrometer
We'll start with the full diagram, and then explain exactly what is going on at each stage.
|
|
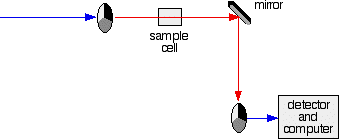
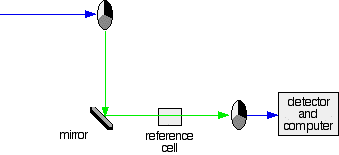
IMPORTANT! The colour-coding of the light beams through the spectrometer is NOT to show that some light is red or blue or green. The colours are simply to emphasise the two different paths that light can take through the device. Where the light is shown as a blue line, this is the path that it will always take. Where it is shown red or green, it will go either one way or the other - depending on how it strikes the rotating disc (see below).
|
Explaining what's happening The light source
You need a light source which gives the entire visible spectrum plus the near ultra-violet so that you are covering the range from about 200 nm to about 800 nm. (This extends slightly into the near infra-red as well.)
|
|
Note: "Near UV" and "near IR" simply means the parts of the UV and IR spectra which are close to the visible spectrum. If you aren't happy about how the various types of electromagnetic radiation relate to each other, follow this link before you go on. Use the BACK button on your browser to return here later.
|
You can't get this range of wavelengths from a single lamp, and so a combination of two is used - a deuterium lamp for the UV part of the spectrum, and a tungsten / halogen lamp for the visible part.
|
|
Note: A deuterium lamp contains deuterium gas under low pressure subjected to a high voltage. It produces a continuous spectrum in the part of the UV spectrum we are interested in.
|
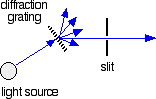
The combined output of these two bulbs is focussed on to a diffraction grating.
The diffraction grating and the slit
You are probably familiar with the way that a prism splits light into its component colours. A diffraction grating does the same job, but more efficiently.
The blue arrows show the way the various wavelengths of the light are sent off in different directions. The slit only allows light of a very narrow range of wavelengths through into the rest of the spectrometer.
By gradually rotating the diffraction grating, you can allow light from the whole spectrum (a tiny part of the range at a time) through into the rest of the instrument.
The rotating discs
This is the clever bit! Each disc is made up of a number of different segments. Those in the machine we are describing have three different sections - other designs may have a different number.
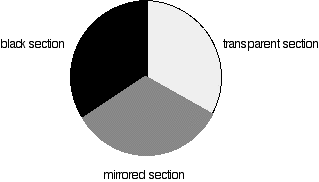
- If it hits the transparent section, it will go straight through and pass through the cell containing the sample. It is then bounced by a mirror onto a second rotating disc.
This disc is rotating such that when the light arrives from the first disc, it meets the mirrored section of the second disc. That bounces it onto the detector.
It is following the red path in the diagram:
- If the original beam of light from the slit hits the mirrored section of the first rotating disc, it is bounced down along the green path. After the mirror, it passes through a reference cell (more about that later).
Finally the light gets to the second disc which is rotating in such a way that it meets the transparent section. It goes straight through to the detector.
- If the light meets the first disc at the black section, it is blocked - and for a very short while no light passes through the spectrometer. This just allows the computer to make allowance for any current generated by the detector in the absence of any light.
The sample and reference cells
These are small rectangular glass or quartz containers. They are often designed so that the light beam travels a distance of 1 cm through the contents.
The sample cell contains a solution of the substance you are testing - usually very dilute. The solvent is chosen so that it doesn't absorb any significant amount of light in the wavelength range we are interested in (200 - 800 nm).
The reference cell just contains the pure solvent.
The detector and computer
The detector converts the incoming light into a current. The higher the current, the greater the intensity of the light.
For each wavelength of light passing through the spectrometer, the intensity of the light passing through the reference cell is measured. This is usually referred to as Io - that's I for Intensity.
The intensity of the light passing through the sample cell is also measured for that wavelength - given the symbol, I.
If I is less than Io, then obviously the sample has absorbed some of the light. A simple bit of maths is then done in the computer to convert this into something called the absorbance of the sample - given the symbol, A.
For reasons which will become clearer when we do a bit of theory on another page, the relationship between A and the two intensities is given by:
On most of the diagrams you will come across, the absorbance ranges from 0 to 1, but it can go higher than that.
An absorbance of 0 at some wavelength means that no light of that particular wavelength has been absorbed. The intensities of the sample and reference beam are both the same, so the ratio Io/I is 1. Log10 of 1 is zero.
An absorbance of 1 happens when 90% of the light at that wavelength has been absorbed - which means that the intensity is 10% of what it would otherwise be.
In that case, Io/I is 100/I0 (=10) and log10 of 10 is 1.
|
|
Note: If you don't feel comfortable with logarithms, don't worry about it. Just accept that an absorbance scale often runs from zero to 1, but could go higher than that in extreme cases (in other words where more than 90% of a wavelength of light is absorbed).
|
The chart recorder
Chart recorders usually plot absorbance against wavelength. The output might look like this:
This particular substance has what are known as absorbance peaks at 255 and 395 nm. How these arise and how they are interpreted are discussed on another page.
-
ESSENTIAL BONDING THEORY FOR UV-VISIBLE ABSORPTION SPECTROMETRY This page takes an introductory look at two areas of bonding theory needed for a proper understanding of how organic compounds absorb some of the UV or visible light that passes through them.
It looks simply at anti-bonding orbitals, and what is meant by conjugation in compounds and how it contributes to the delocalisation of electrons.
It may well be that this page goes in to more detail than your syllabus expects, but it isn't all that difficult and you can't really understand what is going on without it. It would, however, be worth checking your syllabus to find out exactly how much you need to remember.
|
|
Note: If you are studying for a UK-based exam for 16 - 18 year olds, and haven't got a copy of your syllabus, you can find out how to get one by following this link.
|
Anti-bonding orbitals Bonding and anti-bonding orbitals in a simple hydrogen molecule
I am assuming that you know how a simple covalent bond between two atoms forms. Half-filled atomic orbitals on each atom overlap in space to form a new orbital (a molecular orbital) containing both electrons.
|
|
Note: If this is new to you, then you are starting in the wrong place! The simplest place to start on this site is probably to explore a few pages of the organic bonding menu. You need to read at least the first two pages from that menu. Use the BACK button (or HISTORY file or GO menu) on your browser to return here later.
|
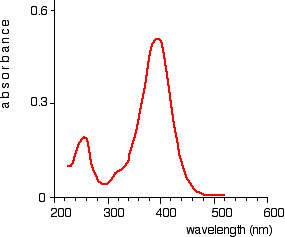
In the case of two hydrogen atoms, each has one electron in the 1s orbital. These come together to make a new orbital surrounding both of the hydrogen nuclei.
It is important to understand exactly what this molecular orbital means. The two electrons are most likely to be found in this region of space - and the most likely place to find them within this space is on the line between the two nuclei.
The molecule holds together because both nuclei are strongly attracted to this same pair of electrons. This most simple of bonds is called a sigma bond - a sigma bond is one where the electron pair is most likely to be found on the line between the two nuclei.
However . . .
This is all a bit of a simplification! Molecular orbital theory demands that if you start with two atomic orbitals, you must end up with two molecular orbitals - and we seem to be only producing one.
A second molecular orbital is formed, but in most cases (including the hydrogen molecule) it is left empty of electrons. It is described as an anti-bonding orbital. The anti-bonding orbital has a quite different shape and energy from the bonding orbital.
The next diagram shows the relative shapes and energies of the various atomic and molecular orbitals when two hydrogen atoms combine.
An anti-bonding orbital is always shown by the use of a star after its symbol.
Notice that when a bonding orbital forms, it is at a lower energy than the original atoms. Energy is released when the bonding orbital is formed, and the hydrogen molecule is more energetically stable than the original atoms.
However, an anti-bonding orbital is less energetically stable than the original atoms.
A bonding orbital is stable because of the attractions between the nuclei and the electrons. In an anti-bonding orbital there are no equivalent attractions - instead you get repulsions. There is very little chance of finding the electrons between the two nuclei - and in fact half-way between the nuclei there is zero chance of finding them. There is nothing to stop the two nuclei from repelling each other apart.
So in the hydrogen case, both of the electrons go into the bonding orbital, because that produces the greatest stability - more stable than having separate atoms, and a lot more stable than having the electrons in the anti-bonding orbital.
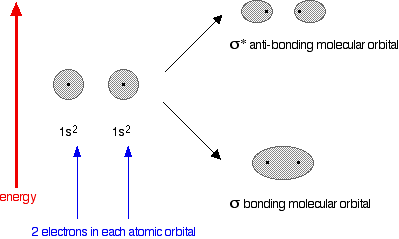
Why doesn't helium form an He2 molecule?
This is just to reinforce the ideas above.
You might reasonably say that helium can't form an He2 molecule because it doesn't have any unpaired electrons to share. Fine! But let's also look at it from the point of molecular orbital theory.
The diagram for helium is just a small modification of the last one.
This time we have a total of 4 electrons in the original atomic orbitals. Two atomic orbitals have to form two molecular orbitals. That means that this time, we would have to use both the bonding and anti-bonding molecular orbitals to accommodate them.
But any gain in energetic stability due to the formation of the bonding orbitals would be countered by the loss of energetic stability because of the anti-bonding ones. There is no energetic advantage in He2 forming - and so it doesn't.
Anti-bonding orbitals in double bonds
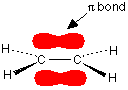
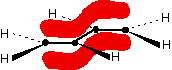
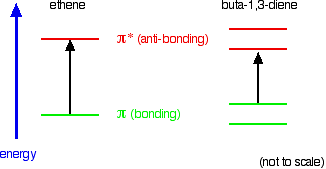
You are probably familiar with a picture of the double bond in ethene shown as:
|
|
Note: Bonds are drawn in various ways to suggest how the atoms are arranged in 3 dimensions. A bond shown with a normal unbroken line is in the plane of the screen or paper. A dotted line shows a bond going away from you. A wedge shows one coming out towards you.
|
The pi bond shown in red is, of course, a normal bonding orbital. It was formed by sideways overlap between a half-filled p-orbital on each of the two carbon atoms. Remember that the two red shapes shown in the diagram are part of the same pi bonding orbital.
But if you overlap two atomic orbitals, you must get two molecular orbitals according to molecular orbital theory. The second one is an anti-bonding pi orbital - and we never draw it under normal circumstances.
The anti-bonding pi orbital is (just like the anti-bonding sigma one) at a higher energy than the bonding orbital - and so isn't used to hold electrons. Both of the electrons in the pi bond are found in the pi bonding orbital.
|
|
Note: If you aren't happy about the diagram of an ethene molecule, read the page about bonding in ethene in the organic bonding section of the site. Use the BACK button on your browser to return here later.
|
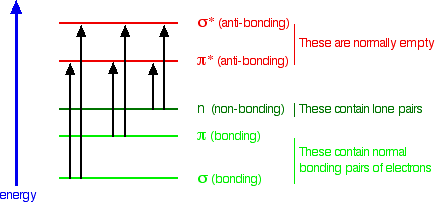
Summarising the relative energies of various kinds of orbitals
The next diagram gives a general impression of how the energies of various types of orbital relate to each other in the sort of compounds we will be looking at when we try to explain the absorption of light. It is not to scale.
You will find that a new sort of orbital has crept into the diagram - labelled "n" (for non-bonding). The sort of non-bonding orbitals that we will be interested in contain lone pairs of electrons on, for example, oxygen, nitrogen and halogen atoms.
So . . . think of non-bonding orbitals as those containing lone pairs of electrons at the bonding level.
|
|
Note: Be careful not to confuse non-bonding with anti-bonding - they mean totally different things. The non-bonding orbitals we are interested in contain a lone pair of electrons - a perfectly stable, filled orbital. Anti-bonding orbitals are normally empty and lower the stability of a compound if they contain electrons. If in doubt, go back and re-read the stuff about anti-bonding orbitals, and be sure that you can see that they have nothing to do with lone pairs.
|
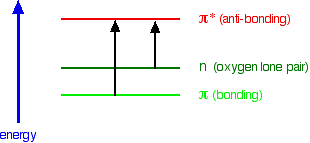
When light passes through a compound, some of the energy in the light kicks an electron from one of the bonding or non-bonding orbitals into one of the anti-bonding ones.
The energy gaps between these levels determine the frequency (or wavelength) of the light absorbed, and those gaps will be different in different compounds. This is covered in detail on another page.
Conjugation We are going to leave explaining what conjugation is for a while - it is necessary to look at some more bonding first.
The simple ethene double bond
To understand about conjugated double bonds, you first need to be sure that you understand simple double bonds.
Ethene contains a simple double bond between two carbon atoms, but the two parts of this bond are different. Part of it is a simple sigma bond formed from end-to-end overlap between orbitals on each carbon atom, and part is caused by sideways overlap between a p-orbital on each carbon.
|
|
Note: If you aren't confident about this, read the page mentioned above about bonding in ethene in the organic bonding section of the site. It is essential that you feel happy about this - otherwise you won't make sense of what comes next. Use the BACK button on your browser to return here later.
|
The important diagram is the one leading up to the formation of the pi bond - where the two p-orbitals are overlapping sideways:
. . . giving the familiar pi bond.
Conjugated double bonds in buta-1,3-diene
Bonding in buta-1,3-diene
Buta-1,3-diene has the structure:
Now picture the formation of the various molecular orbitals as if you were thinking about two ethene molecules joined together. You would have sigma bonds formed by the end-to-end overlap of various orbitals on the carbons and hydrogens. That would leave you with a p-orbital on each carbon atom.
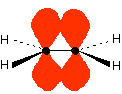
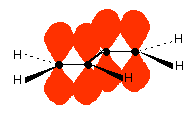
Those p-orbitals will overlap sideways - all of them! A system of delocalised pi bonds is formed, similar to the benzene case that you are probably familiar with. The diagram shows one of those molecular orbitals.
To stress again - the diagram shows only one of the delocalised molecular orbitals. Remember that both of the red bits in the diagram are part of the same orbital.
The interaction of the two double bonds with each other to produce a delocalised system of pi electrons over all four atoms is known as conjugation. Conjugation in this context literally means "joining together".
In reality, if you start by overlapping four atomic orbitals, you will end up with four molecular orbitals. The four electrons will go into the two lowest energy of these - two in each. That means that you get two pi bonding orbitals. We just draw one of these for simplicity - the other one has a different shape.
There are also two pi anti-bonding orbitals, but these are normally empty. For most purposes, we ignore these entirely - although not for this topic because energy from light can promote electrons from a pi bonding orbital into one of the anti-bonding orbitals (as you will see on the next page).
Recognising conjugated double bonds in a molecule
You can recognise the presence of conjugated double bonds in a molecule containing more than one double bond because of the presence of alternating double and single bonds.
The double bonds don't have to be always between carbon atoms. All of the following molecules contain conjugated double bonds, although in the last case, the conjugation doesn't extend over the whole molecule:
However, although the next molecule contains two double bonds, they aren't conjugated. They are separated by two single bonds.
The reason why it is important to have the double and single bonds alternating is that this is the only way you can get all the p-orbitals overlapping sideways. In the last case, you will get sideways overlap at each end of the molecule to get two individual pi bonds. But the extra single bond in the middle stops them from interacting with each other.
Delocalisation extending beyond conjugated double bonds
Benzene rings
You are almost certainly familiar with the delocalisation which occurs in a benzene ring. If you think about benzene using the Kelulé structure, you have a perfect system of alternating single and double bonds around the molecule.
These conjugate to give the familiar delocalised pi system.
Once again, remember that this only shows one of the molecular orbitals formed. There will actually be three bonding pi orbitals and three anti-bonding ones - because they arise from combining a total of six atomic orbitals. The extra bonding orbitals aren't usually drawn.
|
|
Note: If you aren't familiar with this, you will find two pages of Chemguide dealing with the bonding in benzene. One deals with the Kelulé structure, and the other with the modern delocalised structure. You should read both of these pages starting with the one about the Kelulé structure. You will find a link to the second page at the bottom of the first one.
This is likely to take you some time because you will probably have to follow up other links as well in order to fully understand the second page. Don't try to short-cut this.
Use the BACK button (or more likely, the HISTORY file or GO menu) on your browser to return to this page later.
|
Phenylamine and phenol
Delocalisation can also extend beyond pi bonds to include lone pairs on atoms like nitrogen or oxygen. Two simple examples of this are phenylamine (aniline) and phenol.
Writing these using the Kekulé structure for benzene:
You can see the alternating double and single bonds around the benzene ring. This conjugation leads to the familiar delocalised electron system in benzene which we usually show as:
But the delocalisation doesn't stop at the ring. It extends out to the nitrogen or oxygen atoms.
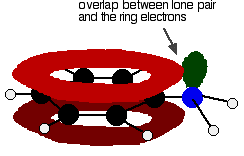
In the phenylamine case, there is a lone pair on the nitrogen atom which can overlap with the ring electrons . . .
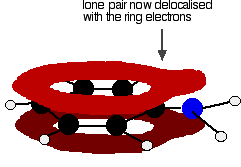
. . . leading to delocalisation which takes in both ring and nitrogen.
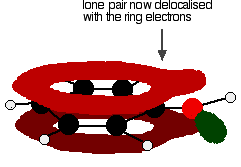
Exactly the same thing happens with phenol. One of the oxygen lone pairs overlaps with the ring electrons. The other one is pointing in the wrong direction to get involved.
So . . . if you are trying to work out how far delocalisation extends in a molecule, don't forget to look for atoms with lone pairs that might get involved in the delocalisation.
Other groups to look out for
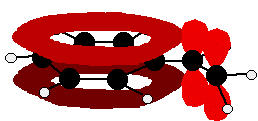
Look especially for benzene rings with groups attached which contain double bonds. Let's start with a couple of simple ones - phenylethene (styrene) and benzaldehyde.
In each case, you've got delocalisation over the ring. Does it extend to the attached group? Do you have anything like alternating single and double bonds?
Yes, you do. You have the double bond in the side group, then a single bond, then the ring delocalisation. Looking at this in the phenylethene case, and imagining the arrangement of orbitals just before delocalisation over the side group:
You can see that the double bond and ring electrons will overlap to form a delocalised system looking something like this:
|
|
Note: Don't panic about learning the shapes of all these delocalised structures. All that matters is that you can recognise the possibility of extensive delocalisation in them. I'm only giving you the details so that you can understand why the delocalisation arises.
|
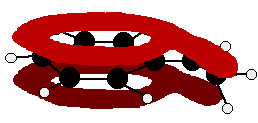
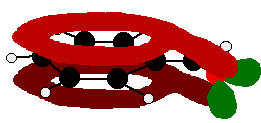
The benzaldehyde case is very similar, except that this time instead of the CH2 group at the end there is an oxygen with two lone pairs. The delocalisation is just the same.
|
|
Note: In fact because of the electronegativity of the oxygen, there is a distortion of the delocalised system towards the oxygen - but that doesn't affect the argument in any way. If you aren't happy about how I got at this structure, have a look at the page about bonding in the carbon-oxygen double bond. Use the BACK button (or the HISTORY file or GO menu) on your browser to return to this page later.
|
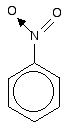
Be careful, though! Remember that to get this extended delocalisation, any double bond in the side chain must be able to conjugate with the ring electrons - the two bits must be close enough to join together.
Molecules like those in the next diagram don't have the delocalisation extending out into the side chain. The extra CH2 group prevents the necessary sideways overlap between the p orbitals of the double bond and the ring electrons.
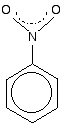
The other side group which it would be useful to know about is the nitro group, NO2 - for example in nitrobenzene.
The bonding in the nitro group is surprisingly awkward to work out. It is often shown with a double bond between the nitrogen and one of the oxygens, and a co-ordinate (dative covalent) bond to the other.
|
|
Note: The bonding in the nitro group is like the bonding in part of a nitric acid molecule which you will find described on the page about co-ordinate (dative covalent) bonds. If you choose to follow this link, use the BACK button on your browser to return to this page later.
|
This structure is actually misleading. Both nitrogen-oxygen bonds are identical and the group already has delocalisation. This is often shown as:
The dotted half-circle suggests the delocalisation. Think of it as being like the circle you draw in the middle of the benzene hexagon.
This delocalisation is just one single bond away from the ring delocalisation. You get conjugation between the two, and the delocalisation takes in the whole molecule.
A case to beware of
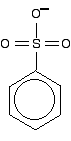
Another case we need to look at (because it occurs in a molecule we'll explore on the next page) is an SO3- group attached to a benzene ring.
It looks as if the double bonds are in just the right position relative to the ring for the delocalisation to extend out over this group. However, I have been told on good authority that the delocalisation doesn't extend from the side group into the ring. I can't, though, find any reference to this anywhere on the web or in the textbooks that I have available.
The bonding in the sulphonate group isn't at all easy to describe in orbital terms. In fact, it is most easily explained in terms of co-ordinate (dative covalent) bonds, but introducing that now is just complicating things pointlessly.
I would hope that you wouldn't get asked a question about delocalisation involving this group at this level. It occurs in methyl orange (discussed on the next page), but its presence there isn't important to the main argument and it can be ignored.
Summary
When you are trying to work out how far delocalisation extends in a molecule, look for:
- alternating double and single bonds - not just between carbon and carbon, but including C=O, C=N, N=N, N=O. Carbon-carbon triple bonds can also be involved in place of a carbon-carbon double bond.
- benzene rings.
- possible involvement of lone pairs on nitrogen or oxygen.
- NO2 groups.
And finally . . . why does all this matter? The wavelength of UV or visible light absorbed by organic compounds depends largely on the extent of delocalisation in the molecules. That means that you may well have to look at an unfamiliar molecule and make a reasonable estimate of whether it is highly delocalised or not very delocalised. It will always be pretty clear-cut at this level, so don't worry too much about it!
You will find lots more about this if you follow the link below to the next page.
UV-VISIBLE ABSORPTION SPECTRA This page explains what happens when organic compounds absorb UV or visible light, and why the wavelength of light absorbed varies from compound to compound.
|
|
Important: If you have come direct to this page from a search engine, you should be aware that it follows on from an introductory page explaining some essential bonding for UV-visible spectrometry. You need to read this before you go on with this page.
|
What happens when light is absorbed by molecules? Promotion of electrons
When we were talking about the various sorts of orbitals present in organic compounds on the introductory page (see above), you will have come across this diagram showing their relative energies:
Remember that the diagram isn't intended to be to scale - it just shows the relative placing of the different orbitals.
When light passes through the compound, energy from the light is used to promote an electron from a bonding or non-bonding orbital into one of the empty anti-bonding orbitals.
|
|
Important: If you don't know exactly what I mean by bonding, non-bonding and anti-bonding orbitals, or don't remember the diagram, go back and read the introductory page again.
|
The possible electron jumps that light might cause are:
In each possible case, an electron is excited from a full orbital into an empty anti-bonding orbital. Each jump takes energy from the light, and a big jump obviously needs more energy than a small one.
Each wavelength of light has a particular energy associated with it. If that particular amount of energy is just right for making one of these energy jumps, then that wavelength will be absorbed - its energy will have been used in promoting an electron.
We need to work out what the relationship is between the energy gap and the wavelength absorbed. Does, for example, a bigger energy gap mean that light of a lower wavelength will be absorbed - or what?
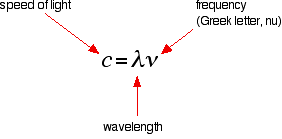
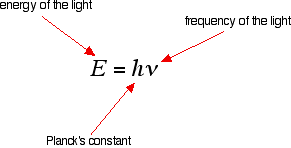
It is easier to start with the relationship between the frequency of light absorbed and its energy:
You can see that if you want a high energy jump, you will have to absorb light of a higher frequency. The greater the frequency, the greater the energy.
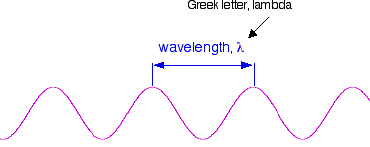
That's easy - but unfortunately UV-visible absorption spectra are always given using wavelengths of light rather than frequency. That means that you need to know the relationship between wavelength and frequency.
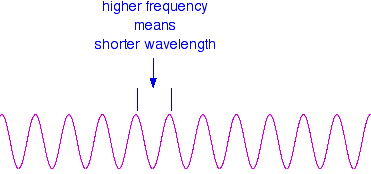
You can see from this that the higher the frequency is, the lower the wavelength is.
So . . . If you have a bigger energy jump, you will absorb light with a higher frequency - which is the same as saying that you will absorb light with a lower wavelength.
Important summary
The larger the energy jump, the lower the wavelength of the light absorbed.
|
|
Note: It is obviously better if you can work this out in case you forget it, but you may feel that it is a lot easier just to learn the last statement. However you do it, you must be confident about this relationship. If you need more help with sorting out these relationships, you will find them discussed more slowly on a page in this section about electromagnetic radiation.
If you choose to follow this link, use the BACK button on your browser to return to this page.
|
Some jumps are more important than others for absorption spectrometry
An absorption spectrometer works in a range from about 200 nm (in the near ultra-violet) to about 800 nm (in the very near infra-red). Only a limited number of the possible electron jumps absorb light in that region.
|
|
Note: If you are interested, there is a description of how a double beam absorption spectrometer works on another page in this section. It isn't necessary to know about this in order to understand the rest of this page.
|
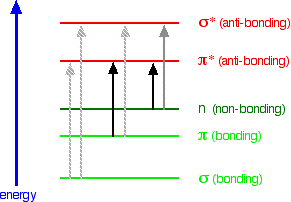
Look again at the possible jumps. This time, the important jumps are shown in black, and a less important one in grey. The grey dotted arrows show jumps which absorb light outside the region of the spectrum we are working in.
Remember that bigger jumps need more energy and so absorb light with a shorter wavelength. The jumps shown with grey dotted arrows absorb UV light of wavelength less that 200 nm.
The important jumps are:
- from pi bonding orbitals to pi anti-bonding orbitals;
- from non-bonding orbitals to pi anti-bonding orbitals;
- from non-bonding orbitals to sigma anti-bonding orbitals.
That means that in order to absorb light in the region from 200 - 800 nm (which is where the spectra are measured), the molecule must contain either pi bonds or atoms with non-bonding orbitals. Remember that a non-bonding orbital is a lone pair on, say, oxygen, nitrogen or a halogen.
Groups in a molecule which absorb light are known as chromophores.
|
|
Note: A Canadian university site describes "chromophore" as "one of those useful but sloppy words whose meaning depends somewhat on the context." As you will find shortly, highly delocalised systems in a molecule are often responsible for absorbing light in the visible region and making the compound look coloured. The delocalisation may involve several different types of group - benzene rings, carbon-carbon double bonds, carbon-oxygen double bonds, lone pairs on nitrogen or oxygen - and so on.
Some people talk as if the whole of the delocalised system was the chromophore; others tend to think on terms of the contributions of individual parts of the system.
It seems to me to be more logical to think in terms of the whole system because it is electron jumps within the system as a whole that cause absorption. If your examiners take a different view, however, obviously you should go with what they want. The only way you will find that out is to look at recent exam papers and mark schemes. If you are a UK A level (or equivalent) student follow this link to the syllabuses page to find out how to get hold of these if you haven't already got them.
|
What does an absorption spectrum look like
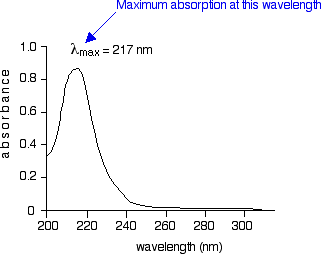
The diagram below shows a simple UV-visible absorption spectrum for buta-1,3-diene - a molecule we will talk more about later. Absorbance (on the vertical axis) is just a measure of the amount of light absorbed. The higher the value, the more of a particular wavelength is being absorbed.
You will see that absorption peaks at a value of 217 nm. This is in the ultra-violet and so there would be no visible sign of any light being absorbed - buta-1,3-diene is colourless. You read the symbol on the graph as "lambda-max".
In buta-1,3-diene, CH2=CH-CH=CH2, there are no non-bonding electrons. That means that the only electron jumps taking place (within the range that the spectrometer can measure) are from pi bonding to pi anti-bonding orbitals.
|
|
Note: The spectrum shown is only a simplified sketch graph - it doesn't pretend to any great accuracy! If you are really wide-awake you might wonder why the graph looks like it does with a broad absorption peak rather than a single line at 217 nm. A jump from a pi bonding orbital to a pi anti-bonding orbital ought to have a fixed energy and therefore absorb a fixed wavelength. The compound is in fact absorbing over a whole range of wavelengths suggesting a whole range of energy jumps.
This problem arises because rotations and vibrations in the molecule are continually changing the energies of the orbitals - and that, of course, means that the gaps between them are continually changing as well. The result is that absorption takes place over a range of wavelengths rather than at one fixed one.
You don't need to worry about this at this level.
|
A chromophore producing two peaks
A chromophore such as the carbon-oxygen double bond in ethanal, for example, obviously has pi electrons as a part of the double bond, but also has lone pairs on the oxygen atom.
That means that both of the important absorptions from the last energy diagram are possible.
|
|
Note: If you aren't too sure about the bonding in a carbon-oxygen double bond, it would be worth following this link before you go on. Use the BACK button on your browser to return to this page when you are ready.
|
You can get an electron excited from a pi bonding to a pi anti-bonding orbital, or you can get one excited from an oxygen lone pair (a non-bonding orbital) into a pi anti-bonding orbital.
|
|
Note: Before you read on, work out which of these will absorb light with the longer wavelength. Try it! If you can work this out for yourself, you have cracked one of the most difficult things about this topic.
|
The non-bonding orbital has a higher energy than a pi bonding orbital. That means that the jump from an oxygen lone pair into a pi anti-bonding orbital needs less energy. That means it absorbs light of a lower frequency and therefore a higher wavelength.
Ethanal can therefore absorb light of two different wavelengths:
- the pi bonding to pi anti-bonding absorption peaks at 180 nm;
- the non-bonding to pi anti-bonding absorption peaks at 290 nm.
Both of these absorptions are in the ultra-violet, but most spectrometers won't pick up the one at 180 nm because they work in the range from 200 - 800 nm.
The importance of conjugation and delocalisation in what wavelength is absorbed
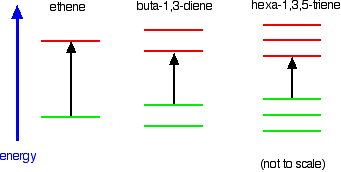
Consider these three molecules:
Ethene contains a simple isolated carbon-carbon double bond, but the other two have conjugated double bonds. In these cases, there is delocalisation of the pi bonding orbitals over the whole molecule.
|
|
Important: If you don't know understand about conjugation, go back and read that section of the introductory page again.
|
Now look at the wavelengths of the light which each of these molecules absorbs.
| molecule | wavelength of maximum absorption (nm) |
|---|
| ethene | 171 |
| buta-1,3-diene | 217 |
| hexa-1,3,5-triene | 258 |
All of the molecules give similar UV-visible absorption spectra - the only difference being that the absorptions move to longer and longer wavelengths as the amount of delocalisation in the molecule increases.
Why is this?
You can actually work out what must be happening.
- The maximum absorption is moving to longer wavelengths as the amount of delocalisation increases.
- Therefore maximum absorption is moving to shorter frequencies as the amount of delocalisation increases.
- Therefore absorption needs less energy as the amount of delocalisation increases.
- Therefore there must be less energy gap between the bonding and anti-bonding orbitals as the amount of delocalisation increases.
. . . and that's what is happening.
Compare ethene with buta-1,3-diene. In ethene, there is one pi bonding orbital and one pi anti-bonding orbital. In buta-1,3-diene, there are two pi bonding orbitals and two pi anti-bonding orbitals. This is all discussed in detail on the introductory page that you should have read.
The highest occupied molecular orbital is often referred to as the HOMO - in these cases, it is a pi bonding orbital. The lowest unoccupied molecular orbital (the LUMO) is a pi anti-bonding orbital.
Notice that the gap between these has fallen. It takes less energy to excite an electron in the buta-1,3-diene case than with ethene.
In the hexa-1,3,5-triene case, it is less still.
|
|
Note: In this case, you will have to work out for yourself why there are 3 bonding and 3 anti-bonding pi orbitals in the hexa-1,3,5-triene. If you are interested, you can work it out in the same way that I have used for buta-1,3-diene on the introductory page. It isn't essential that you do this - all that matters is that you can see the pattern - the more the delocalisation, the longer the wavelength absorbed. If you choose to follow this link, use the BACK button on your browser to come back here again later.
|
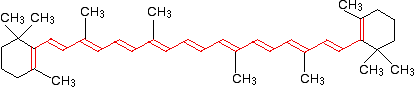
If you extend this to compounds with really massive delocalisation, the wavelength absorbed will eventually be high enough to be in the visible region of the spectrum, and the compound will then be seen as coloured. A good example of this is the orange plant pigment, beta-carotene - present in carrots, for example.
Why is beta-carotene orange?
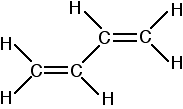
Beta-carotene has the sort of delocalisation that we've just been looking at, but on a much greater scale with 11 carbon-carbon double bonds conjugated together. The diagram shows the structure of beta-carotene with the alternating double and single bonds shown in red.
The more delocalisation there is, the smaller the gap between the highest energy pi bonding orbital and the lowest energy pi anti-bonding orbital. To promote an electron therefore takes less energy in beta-carotene than in the cases we've looked at so far - because the gap between the levels is less.
Remember that less energy means a lower frequency of light gets absorbed - and that's equivalent to a longer wavelength.
Beta-carotene absorbs throughout the ultra-violet region into the violet - but particularly strongly in the visible region between about 400 and 500 nm with a peak about 470 nm.
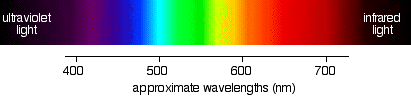
If you have read the page in this section about electromagnetic radiation, you might remember that the wavelengths associated with the various colours are approximately:
| colour region | wavelength (nm) |
|---|
| violet | 380 - 435 |
| blue | 435 - 500 |
| cyan | 500 - 520 |
| green | 520 - 565 |
| yellow | 565 - 590 |
| orange | 590 - 625 |
| red | 625 - 740 |
So if the absorption is strongest in the violet to cyan region, what colour will you actually see? It is tempting to think that you can work it out from the colours that are left - and in this particular case, you wouldn't be far wrong. Unfortunately, it isn't as simple as that!
Sometimes what you actually see is quite unexpected. Mixing different wavelengths of light doesn't give you the same result as mixing paints or other pigments.
You can, however, sometimes get some estimate of the colour you would see using the idea of complementary colours.
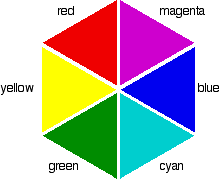
Complementary colours
If you arrange some colours in a circle, you get a "colour wheel". The diagram shows one possible version of this. An internet search will throw up many different versions!
Colours directly opposite each other on the colour wheel are said to be complementary colours. Blue and yellow are complementary colours; red and cyan are complementary; and so are green and magenta.
Mixing together two complementary colours of light will give you white light.
|
|
Beware: That is NOT the same as mixing together paint colours. If you mix yellow and blue paint you don't get white paint. Is this confusing? YES!
|
What this all means is that if a particular colour is absorbed from white light, what your eye detects by mixing up all the other wavelengths of light is its complementary colour.
In the beta-carotene case, the situation is more confused because you are absorbing such a range of wavelengths. However, if you think of the peak absorption running from the blue into the cyan, it would be reasonable to think of the colour you would see as being opposite that where yellow runs into red - in other words, orange.
You will find the colours a bit more clear-cut in the other two examples we'll talk about below.
|
|
|
Applying this to the colour changes of two indicators Phenolphthalein
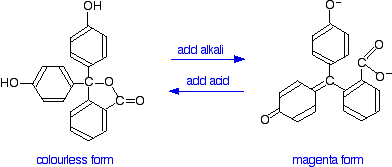
You have probably used phenolphthalein as an acid-base indicator, and will know that it is colourless in acidic conditions and magenta (bright pink) in an alkaline solution. How is this colour change related to changes in the molecule?
The structures of the two differently coloured forms are:
Both of these absorb light in the ultra-violet, but the one on the right also absorbs in the visible with a peak at 553 nm.
The molecule in acid solution is colourless because our eyes can't detect the fact that some light is being absorbed in the ultra-violet. However, our eyes do detect the absorption at 553 nm produced by the form in alkaline solution.
553 nm is in the green region of the spectrum. If you look back at the colour wheel, you will find that the complementary colour of green is magenta - and that's the colour you see.
So why does the colour change as the structure changes?
What we have is a shift to absorption at a higher wavelength in alkaline solution. As we've already seen, a shift to higher wavelength is associated with a greater degree of delocalisation.
Here is a modified diagram of the structure of the form in acidic solution - the colourless form. The extent of the delocalisation is shown in red.
Notice that there is delocalisation over each of the three rings - extending out over the carbon-oxygen double bond, and to the various oxygen atoms because of their lone pairs.
But the delocalisation doesn't extend over the whole molecule. The carbon atom in the centre with its four single bonds prevents the three delocalised regions interacting with each other.
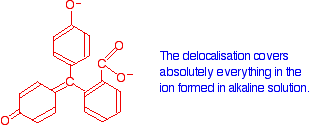
Now compare that with the magenta form:
The rearrangement now lets the delocalisation extend over the entire ion. This greater delocalisation lowers the energy gap between the highest occupied molecular orbital and the lowest unoccupied pi anti-bonding orbital. It needs less energy to make the jump and so a longer wavelength of light is absorbed.
Remember: Increasing the amount of delocalisation shifts the absorption peak to a higher wavelength.
|
|
Note: Don't panic at the thought that you might have to draw these structures in an exam. At UK A level (and its equivalent) standard, it won't happen. However, if you were given the structures of the two forms of phenolphthalein and asked to explain the colour change, that could make a good question (depending, of course, on what exactly your syllabus expects you to be able to do).
|
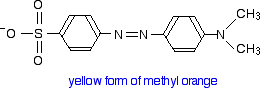
Methyl orange
You will know that methyl orange is yellow in alkaline solutions and red in acidic ones.
The structure in alkaline solution is:
In acid solution, a hydrogen ion is (perhaps unexpectedly) picked up on one of the nitrogens in the nitrogen-nitrogen double bond.
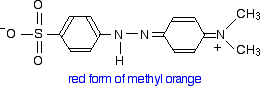
This now gets a lot more complicated! The positive charge on the nitrogen is delocalised (spread around over the structure) - especially out towards the right-hand end of the molecule as we've written it. The normally drawn structure for the red form of methyl orange is . . .
But this can be seriously misleading as regards the amount of delocalisation in the structure for reasons discussed below (after the red warning box) if you are interested.
|
|
|
So which is the more delocalised structure - red or yellow?
Let's work backwards from the absorption spectra to see if that helps.
The yellow form has an absorption peak at about 440 nm. That's in the blue region of the spectrum, and the complementary colour of blue is yellow. That's exactly what you would expect.
The red form has an absorption peak at about 520 nm. That's at the edge of the cyan region of the spectrum, and the complementary colour of cyan is red. Again, there's nothing unexpected here.
Notice that the change from the yellow form to the red form has produced an increase in the wavelength absorbed. An increase in wavelength suggests an increase in delocalisation.
That means that there must be more delocalisation in the red form than in the yellow one.
Why? For the purposes of UK A level (and its equivalents), that's probably unanswerable. However, if you are interested, there's a possible answer below . . .
|
|
|
Here again is the structure of the yellow form:
Delocalisation will extend over most of the structure - out as far as the lone pair on the right-hand nitrogen atom.
If you use the normally written structure for the red form, the delocalisation seems to be broken in the middle - the pattern of alternating single and double bonds seems to be lost.
But that is to misunderstand what this last structure represents.
Canonical forms
If you draw the two possible Kekulé structures for benzene, you will know that the real structure of benzene isn't like either of them. The real structure is somewhere between the two - all the bonds are identical and somewhere between single and double in character. That's because of the delocalisation in benzene.
The two structures are known as canonical forms, and they can each be thought of as adding some knowledge to the real structure. For example, the bond drawn at the top right of the molecule is neither truly single or double, but somewhere in between. Similarly with all the other bonds.
|
|
Note: If you haven't come across canonical forms as a way of representing delocalisation, it is important that you don't imagine that the molecule is rapidly flipping from one structure to another. The double-headed arrows mean something different. A mule is a hybrid of a donkey and a horse. In this notation, you could represent a mule by writing donkey and horse connected by a double-headed arrow. Neitherdonkey nor horse accurately represents what a mule looks like, but with a bit of imagination you could build up a fairly good picture of a mule by combining together the characteristics of both donkey and horse. But a mule obviously doesn't spend its time rapidly changing back and forth between being a donkey and a horse!
|
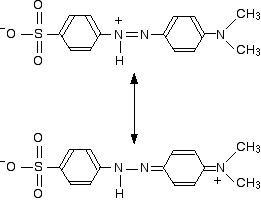
The two structures we've previously drawn for the red form of methyl orange are also canonical forms - two out of lots of forms that could be drawn for this structure. We could represent the delocalised structure by:
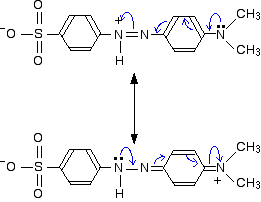
These two forms can be thought of as the result of electron movements in the structure, and curly arrows are often used to show how one structure can lead to the other.
In reality, the electrons haven't shifted fully either one way or the other. Just as in the benzene case, the actual structure lies somewhere in between these.
You must also realise that drawing canonical forms has no effect on the underlying geometry of the structure. Bond types or lengths or angles don't change in the real structure.
For example, the lone pairs on the nitrogen atoms shown in the last diagram are both involved with the delocalisation. For this to happen all the bonds around these nitrogens must be in the same plane, with the lone pair sticking up so that it can overlap sideways with orbitals on the next-door atoms. The fact that in each of the two canonical forms one of these nitrogens is shown as if it had an ammonia-like arrangement of the bonds is potentially misleading - and makes it look as if the delocalisation is broken.
The problem is that there is no easy way of representing a complex delocalised structure in simple structural diagrams. It is bad enough with benzene - with something as complicated as methyl orange any method just leads to possible confusion if you aren't used to working with canonical forms.
It gets even more complicated! If you were doing this properly there would be a host of other canonical forms with different arrangements of double and single bonds and with the positive charge located at various places around the rings and on the other nitrogen atom.
The real structure can't be represented properly by any one of this multitude of canonical forms, but each gives a hint of how the delocalisation works.
If we take the two forms we have written as perhaps the two most important ones, it suggests that there is delocalisation of the electrons over the whole structure, but that electron density is a bit low around the two nitrogens carrying the positive charge on one canonical form or the other.
So why is the red form more delocalised than the yellow one?
Finally, we get around to an attempt at an explanation as to why the delocalisation is greater in the red form of methyl orange in acid solution than in the yellow one in alkaline solution.
The answer may lie in the fact that the lone pair on the nitrogen at the right-hand end of the structure as we've drawn it is more fully involved in the delocalisation in the red form. The canonical form with the positive charge on that nitrogen suggests a significant movement of that lone pair towards the rest of the molecule.
Doesn't the same thing happen to the lone pair on the same nitrogen in the yellow form of methyl orange? Not to the same extent.
Any canonical form that you draw in which that happens produces another negatively charged atom somewhere in the rest of the structure. Separating negative and positive charges like this is energetically unfavourable. In the red form, we aren't producing a new separation of charge - just shifting a positive charge around the structure.
Please remember: This is high-level stuff. To really understand it you need to have met canonical forms before and practised drawing them. This is degree level chemistry and not A level (or its equivalent). You do NOT need any of this (from below the red warning) unless perhaps you are reading this as a university student.
-
THE BEER-LAMBERT LAW This page takes a brief look at the Beer-Lambert Law and explains the use of the terms absorbance and molar absorptivity relating to UV-visible absorption spectrometry.
Absorbance Measuring the absorbance of a solution
If you have read the page about how an absorption spectrometer works, you will know that it passes a whole series of wavelengths of light through a solution of a substance (the sample cell) and also through an identical container (the reference cell) which only has solvent in it.
|
|
Note: It isn't essential to read about how the spectrometer works, but you could follow this link if you are interested or if it is on your syllabus. Everything you need from that page to understand the present topic is repeated below.
|
For each wavelength of light passing through the spectrometer, the intensity of the light passing through the reference cell is measured. This is usually referred to as Io - that's I for Intensity.
The intensity of the light passing through the sample cell is also measured for that wavelength - given the symbol, I.
If I is less than Io, then obviously the sample has absorbed some of the light. A simple bit of maths is then done in the computer to convert this into something called the absorbance of the sample - given the symbol, A.
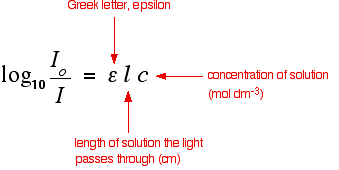
For reasons to do with the form of the Beer-Lambert Law (below), the relationship between A (the absorbance) and the two intensities is given by:
On most of the diagrams you will come across, the absorbance ranges from 0 to 1, but it can go higher than that.
An absorbance of 0 at some wavelength means that no light of that particular wavelength has been absorbed. The intensities of the sample and reference beam are both the same, so the ratio Io/I is 1. Log10 of 1 is zero.
An absorbance of 1 happens when 90% of the light at that wavelength has been absorbed - which means that the intensity is 10% of what it would otherwise be.
In that case, Io/I is 100/I0 (=10) and log10 of 10 is 1.
|
|
Note: If you don't feel comfortable with logarithms, don't worry about it. Just accept that an absorbance scale often runs from zero to 1, but could go higher than that in extreme cases (in other words where more than 90% of a wavelength of light is absorbed).
|
Absorbance isn't very good for making comparisons
The importance of concentration
The proportion of the light absorbed will depend on how many molecules it interacts with. Suppose you have got a strongly coloured organic dye. If it is in a reasonably concentrated solution, it will have a very high absorbance because there are lots of molecules to interact with the light.
However, in an incredibly dilute solution, it may be very difficult to see that it is coloured at all. The absorbance is going to be very low.
Suppose then that you wanted to compare this dye with a different compound. Unless you took care to make allowance for the concentration, you couldn't make any sensible comparisons about which one absorbed the most light.
The importance of the container shape
Suppose this time that you had a very dilute solution of the dye in a cube-shaped container so that the light travelled 1 cm through it. The absorbance isn't likely to be very high. On the other hand, suppose you passed the light through a tube 100 cm long containing the same solution. More light would be absorbed because it interacts with more molecules.
Again, if you want to draw sensible comparisons between solutions, you have to allow for the length of the solution the light is passing through.
Both concentration and solution length are allowed for in the Beer-Lambert Law.
The Beer-Lambert Law What the Law looks like
You will find that various different symbols are given for some of the terms in the equation - particularly for the concentration and the solution length. I'm going to use the obvious form where the concentration of the solution is "c" and the length is "l".
|
|
Note: That's obviously "l" for length. The font I'm using won't distinguish between "l" for length and a capital letter "I" (for Intensity). That problem disappears in the equation below - where it is obvious which is which.
|
You should recognise the expression on the left of this equation as what we have just defined as the absorbance, A. You might also find the equation written in terms of A:
That's obviously easier to remember than the first one, but you would still have to learn the equation for absorbance. It might be useful to learn it in the form:
The Greek letter epsilon in these equations is called the molar absorptivity - or sometimes the molar absorption coefficient.
Molar absorptivity
If you rearrange the simplest of the equations above to give an expression for epsilon (the molar absorptivity), you get:
Remember that the absorbance of a solution will vary as the concentration or the size of the container varies. Molar absorptivity compensates for this by dividing by both the concentration and the length of the solution that the light passes through. Essentially, it works out a value for what the absorbance would be under a standard set of conditions - the light travelling 1 cm through a solution of 1 mol dm-3.
That means that you can then make comparisons between one compound and another without having to worry about the concentration or solution length.
Values for molar absorptivity can vary hugely. For example, ethanal has two absorption peaks in its UV-visible spectrum - both in the ultra-violet. One of these corresponds to an electron being promoted from a lone pair on the oxygen into a pi anti-bonding orbital; the other from a pi bonding orbital into a pi anti-bonding orbital.
|
|
|
The table gives values for the molar absorptivity of a solution of ethanal in hexane. Notice that there are no units given for absorptivity. That's quite common. If you want them, and assuming the length is in cm and the concentration is mol dm-3, the units are mol-1 dm3 cm-1.
| electron jump | wavelength of maximum absorption (nm) | molar absorptivity |
|---|
| lone pair to pi anti-bonding orbital | 290 | 15 |
| pi bonding to pi anti-bonding orbital | 180 | 10000 |
The ethanal obviously absorbs much more strongly at 180 nm than it does at 290 nm. (Although, in fact, the 180 nm absorption peak is outside the range of most spectrometers.)
You may come across diagrams of absorption spectra plotting absorptivity on the vertical axis rather than absorbance. However, if you look at the figures above and the scales that are going to be involved, you aren't really going to be able to spot the absorption at 290 nm. It will be a tiny little peak compared to the one at 180 nm.
To get around this, you may also come across diagrams in which the vertical axis is plotted as log10(molar absorptivity).
If you take the logs of the two numbers in the table, 15 becomes 1.18, while 10000 becomes 4. That makes it possible to plot both values easily, but produces strangely squashed-looking spectra!
USING UV-VISIBLE ABSORPTION SPECTRA This page takes a brief look at how UV-visible absorption spectra can be used to help identify compounds and to measure the concentrations of coloured solutions. It assumes that you know how these spectra arise, and know what is meant by terms such as absorbance, molar absorptivity and lambda-max. You also need to be familiar with the Beer-Lambert Law.
|
|
Important: If you don't know about these things, this page is a waste of your time! Explore the rest of the UV-visible spectroscopy menu before you go on.
|
Using UV-absorption spectra to help identify organic compounds
If you have worked through the rest of this section, you will know that the wavelength of maximum absorption (lambda-max) depends on the presence of particular chromophores (light-absorbing groups) in a molecule.
For example, on another page you will have come across the fact that a simple carbon-carbon double bond (for example in ethene) has a maximum absorption at 171 nm. The two conjugated double bonds in buta-1,3-diene have a maximum absorption at a longer wavelength of 217 nm.
We also talked about the two peaks in the spectrum of ethanal (containing a simple carbon-oxygen double bond) at 180 and 290 nm.
In carefully chosen simple cases (which is all you will get at this level), if you compared the peaks on a given UV-visible absorption spectrum with a list of known peaks, it would be fairly easy to pick out some structural features of an unknown molecule.
Lists of known peaks often include molar absorptivity values as well. That might help you to be even more sure. For example (again using the simple carbon-oxygen double bond), data shows that the peak at 290 has a molar absorptivity of only 15, compared with the one at 180 of 10000.
If your spectrum showed a very large peak at 180, and an extremely small one at 290, that just adds to your certainty.
Any question set at this level is going to be so trivial, and so obvious, that it isn't worth spending any more time on this. Let's look at something a bit more complicated!
Using UV-absorption spectra to find concentrations
You should remember the Beer-Lambert Law:
The expression on the left of the equation is known as the absorbance of the solution and is measured by a spectrometer. The equation is sometimes written in terms of that absorbance.
The symbol epsilon is the molar absorptivity of the solution.
|
|
|
Finding concentration using the molar absorptivity
If you know the molar absorptivity of a solution at a particular wavelength, and you measure the absorbance of the solution at that wavelength, it is easy to calculate the concentration. The only other variable in the expression above is the length of the solution. That's easy to measure and, in fact, the cell containing the solution may well have been manufactured with a known length of 1 cm.
For example, let's suppose you have a solution in a cell of length 1 cm. You measure the absorbance of the solution at a particular wavelength using a spectrometer. The value is 1.92. You find a value for molar absorptivity in a table of 19400 for that wavelength.
Substituting those values:
Notice what a very low concentration can be measured provided you are working with a substance with a very high molar absorptivity.
This method, of course, depends on you having access to an accurate value of molar absorptivity. It also assumes that the Beer-Lambert Law works over the whole concentration range (not true!).
It is much better to measure the concentration by plotting a calibration curve. It saves doing any calculations for one thing!
Finding concentration by plotting a calibration curve
Doing it this way you don't have to rely on a value of molar absorptivity, the reliability of the Beer-Lambert Law, or even know the dimensions of the cell containing the solution.
What you do is make up a number of solutions of the compound you are investigating - each of accurately known concentration. Those concentrations should bracket the concentration you are trying to find - some less concentrated; some more concentrated. With coloured solutions, this isn't a problem. You would just make up some solutions which are a bit lighter and some a bit darker in colour.
For each solution, you measure the absorbance at the wavelength of strongest absorption - using the same container for each one. Then you plot a graph of that absorbance against concentration. This is a calibration curve.
According to the Beer-Lambert Law, absorbance is proportional to concentration, and so you would expect a straight line. That is true as long as the solutions are dilute, but the Law breaks down for solutions of higher concentration, and so you might get a curve under these circumstances.
As long as you are working from values either side of the one you are trying to find, that isn't a problem.
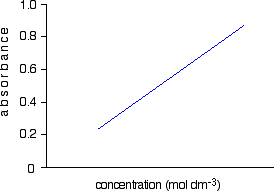
Having drawn a best fit line, the calibration curve will probably look something like the next diagram. (I've drawn it as a straight line because it is easier for me to draw than a curve(!), and it's what you will probably get if you are working with really dilute solutions. But if it turns out to be a curve, so be it!)
Notice that no attempt has been made to force the line back through the origin. If the Beer-Lambert Law worked perfectly, it would pass through the origin, but you can't guarantee that it is working properly at the concentrations you are using.
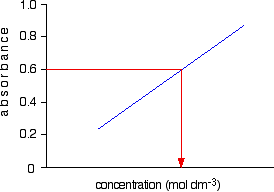
Now all you have to do is to measure the absorbance of the solution with the unknown concentration at the same wavelength. If, for example, it had an absorbance of 0.600, you can just read the corresponding concentration from the graph as below.
|
|
| |
|
|
|
|
|
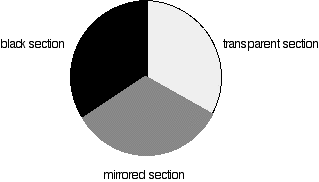
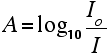


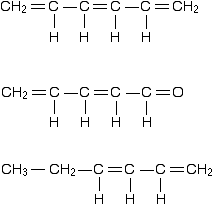

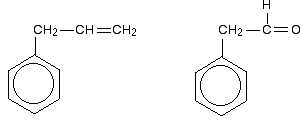
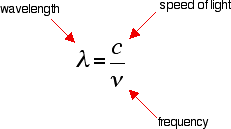
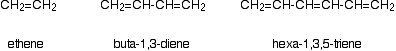

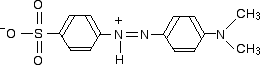
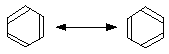
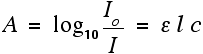
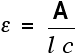
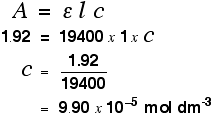
No comments:
Post a Comment